Abstract
Research Article
Study the effect of transient vibration on multi-storey building structure according to equivalent spring-mass system performed by Ansys
Anosh Kujur* and Dinesh Sen
Published: 16 April, 2019 | Volume 3 - Issue 1 | Pages: 011-024
The carried work has based on transient vibration response of multiple degrees of freedom (MDOF) system. By this work study of Time–history analysis and prediction of the displacement for excitation has done. For the MDOF system, we have taken the four-storey building to done transient vibration. We establish the equivalent spring-mass system. Transient analysis has done for both Undamped and Damped of the forced system of multiple degrees of freedom (MDOF) system. In the case of the Damped system, we have done three stages of damping, i.e., (1) Underdamped system, (2) Critically damped system, (3) Overdamped system. The time-history graph obtained for two different time stages i.e. 0.001 sec & 0.01 sec with initial time 0.000001 sec. The natural frequency has determined by both theoretical calculation and ANSYS. The whole study of transient vibration makes it possible to predict the damping values that oppose any kind of sudden impact or force vibration, such as blasts, earthquakes and tsunamis. The ANSYS is the modelling and simulation software is used to perform the transient vibration response. The Mode Superposition method is used by ANSYS to calculate the structure response
Read Full Article HTML DOI: 10.29328/journal.acee.1001013 Cite this Article Read Full Article PDF
Keywords:
Transient vibration response; MDOF; Time-history graph; Excitation; Spring-mass system; Undamped of forced system; Damped of forced system; Underdamped system; Critically damped system; Overdamped system; Natural frequency; Modelling and Simulation; ANSYS; Mode superposition method
References
- Chopra AK. Multi-Degree-of-Freedom Systems. Dynamics of Structures: Theory and Applications to Earthquake Engineering. Pearson Education, Inc., Prentice Hall, One Lake Street, Upper Saddle River, NJ. 1995; 347-392. Ref.: http://tinyurl.com/y4d8htph
- Damodarasamy SR, Kavitha S. Basics of Structural Dynamics and Aseismic Design. Multiple Degrees of Freedom Systems. PHE Learning Private Limited, New Delhi. 2005; 158-165. Ref.: http://tinyurl.com/y5d73yqq
- Agarwal P, Shrikhande M. Earthquake Resistant Design of Structures. Dynamics of Multi-Degree-of-Freedom Systems. Prentice Hall of India, New Delhi. 2015; 156-187.
- Paz M. Structural Dynamics-Theory and Computation. Response to General Dynamic Loading. CBS Publishers and Distributors, New Delhi. 1996; 101-140. Ref.: http://tinyurl.com/y5uv6nf3
- Wright JR, Cooper JE. Introduction to Aircraft Aeroelasticity and Loads. Vibration of Multiple Degree of Freedom Systems’, John Wiley & Sons, Ltd. 2015; 27-47. Ref.: http://tinyurl.com/y3ly69tc
- Rao SS. Mechanical Vibrations. Multidegree-of-Freedom Systems. Pearson Education, Inc., Prentice Hall, 1 Lake Street, Upper Saddle River, NJ. 2004; 553-623. Ref.: http://tinyurl.com/y4c5rrgm
- Clough RW, Penzien J. Dynamics of Structures. Multi-Degree-of-Freedom Systems. McGraw-Hill, New York. 1993; 169-179. Ref.: http://tinyurl.com/yyeqshl6
- Graham Kelly S. Mechanical Vibrations: Theory and Applications. Modeling of MDOF System. Cengage Learning, First Stamford Place, Stamford, USA. 2012; 459-506. Ref.: http://tinyurl.com/y27t5tjm
Figures:
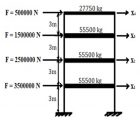
Figure 1
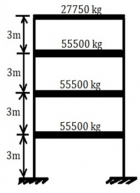
Figure 2
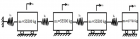
Figure 3
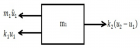
Figure 4
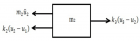
Figure 5
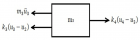
Figure 6
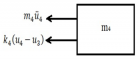
Figure 7

Figure 8
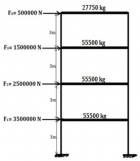
Figure 9
Figure 10
Figure 11
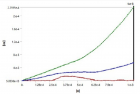
Figure 12
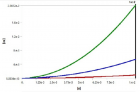
Figure 13
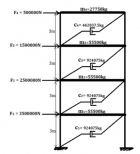
Figure 14
Figure 15
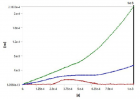
Figure 16
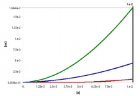
Figure 17
Figure 18
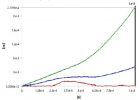
Figure 19
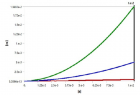
Figure 20

Figure 21
Similar Articles
-
Study the effect of transient vibration on multi-storey building structure according to equivalent spring-mass system performed by AnsysAnosh Kujur*,Dinesh Sen. Study the effect of transient vibration on multi-storey building structure according to equivalent spring-mass system performed by Ansys. . 2019 doi: 10.29328/journal.acee.1001013; 3: 011-024
Recently Viewed
-
Microcystic Meningioma: Atypical Meningioma Revisited. Rare Case Report with Review of LiteratureKaustubh Gupta*. Microcystic Meningioma: Atypical Meningioma Revisited. Rare Case Report with Review of Literature. J Radiol Oncol. 2025: doi: 10.29328/journal.jro.1001079; 9: 046-049
-
Maternal and perinatal outcomes of uterine rupture in Lubumbashi, Democratic Republic of CongoJacques Ngoy Kitenge,Olivier Mukuku*,Xavier K Kinenkinda,Prosper L Kakudji. Maternal and perinatal outcomes of uterine rupture in Lubumbashi, Democratic Republic of Congo. Clin J Obstet Gynecol. 2020: doi: 10.29328/journal.cjog.1001067; 3: 136-141
-
Do Fishes Hallucinate Human Folks?Dinesh R*,Sherry Abraham,Kathiresan K,Susitharan V,Jeyapavithran C,Paul Nathaniel T,Siva Ganesh P. Do Fishes Hallucinate Human Folks?. Arch Food Nutr Sci. 2017: doi: 10.29328/journal.afns.1001003; 1: 020-023
-
Assessment of Redox Patterns at the Transcriptional and Systemic Levels in Newly Diagnosed Acute LeukemiaAna Carolina Agüero Aguilera, María Eugenia Mónaco, Sandra Lazarte, Emilse Ledesma Achem, Natalia Sofía Álvarez Asensio, Magdalena María Terán, Blanca Alicia Issé, Marcela Medina, Cecilia Haro*. Assessment of Redox Patterns at the Transcriptional and Systemic Levels in Newly Diagnosed Acute Leukemia. J Hematol Clin Res. 2024: doi: 10.29328/journal.jhcr.1001029; 8: 017-023
-
Assessment of Indigenous Knowledge on Using of Traditional Medicinal Plants to Cure Human Diseases in South Omo Zone Baka Dawla Ari District, Kure and Bitsmal South EthiopiaGizaw Bejigo*. Assessment of Indigenous Knowledge on Using of Traditional Medicinal Plants to Cure Human Diseases in South Omo Zone Baka Dawla Ari District, Kure and Bitsmal South Ethiopia. J Plant Sci Phytopathol. 2024: doi: 10.29328/journal.jpsp.1001132; 8: 048-054
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."